J’écris cet article en ce moment, revenez régulièrement pour voir ma progression.
Les centrales inertielles sont des composants courants de notre quotidien: application « Niveau à bulle » sur nos smartphones, drone de loisir ou encore avion de ligne, ces composants permettent à un système d’avoir une certaine autonomie pour se repérer dans l’espace. Améliorés soit par l’utilisation d’une physique poussée, ou par des traitements du signal très avancés, ils peuvent aller de quelques dollars à plusieurs centaines de milliers, la différence majeure tenant dans leur « dérive« . Nous allons nous intéresser à ces composants, leurs concepts intrinsèques et chercher à atteindre la meilleure dérive atteinte à ce jour avec un des composants les moins chers du marché: le MPU6050 (0.52 cents …)
Le MPU6050
Le MPU6050 est un capteur dit 6DOF pour 6 degress of freedom. Il restitue la mesure de 6 degrés de libertés: accélération selon ses propres axes X, Y, Z et vitesse de rotation autour de ses axes X, Y et Z. Il mesure les accélérations jusqu’à +-16g, mais peut se régler sur des plages plus fines ±2 g, ±4 g, ±8 g, ±16 g.

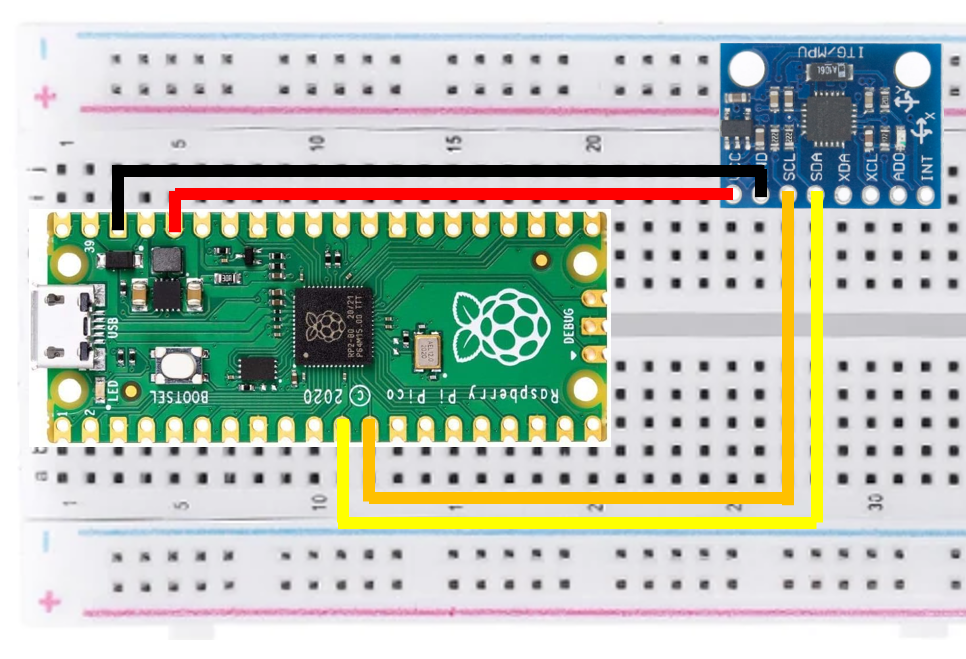
Il communique selon le protocole I2C, on retrouve donc les pins SDA et SCL pour échanger les mesures. Les pins VCC et GND pour l’alimentation (3-5V, un régulateur est intégré au PCB) et la masse. Les pins XDA et XCL servent à rajouter un senseur tiers et faire exploiter ses mesures pa rle MPU6050, on ne s’en servira pas ici. Le pin INT sert aux interruptions qui peuvent être envoyée du MPU6050 vers votre microcontrôleur.
Raspberry Pi Pico et MPU6050: affichage des premières mesures brutes
On va commencer par un montage simple pour prendre en main ce composant.
Pour mettre en œuvre ce montage, on va utiliser une librairie qui permet d’adresser le MPU6050 en MicroPython. On récupère les fichiers imu.py et vector3d.py ici: https://github.com/micropython-IMU/micropython-mpu9x50
Dans le même répertoire, on va enregistrer le fichier main.py avec le contenu suivant:
from imu import MPU6050
import time
from machine import Pin, I2C
i2c = I2C(0, sda=Pin(8), scl=Pin(9), freq=400000)
imu = MPU6050(i2c)
while True:
accel = imu.accel
gyro = imu.gyro
print("{:0.2f}".format(accel.x), "\t", "{:0.2f}".format(accel.y), "\t", "{:0.2f}".format(accel.z), end="\t")
print ("{:0.2f}".format(gyro.x), "\t", "{:0.2f}".format(gyro.y), "\t", "{:0.2f}".format(gyro.z))
time.sleep(0.01)
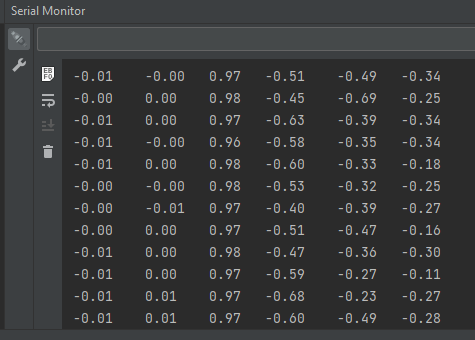
On téléverse les trois fichiers sur le Pico et on ouvre un terminal série connecté au Pico. On obtient alors une série de valeurs qui défilent.
Sur chaque ligne, on affiche les trois composantes de l’accélération X, Y, Z en g (1g ~ 0.98 m.s-2), puis les trois mesures du gyroscope selon X, Y, Z en deg.s-1. Tout fonctionne, on va pouvoir passer à l’utilisation de ces valeurs.
Intégration et gravité
Pour cette première expérience, on va adopter le protocole suivant. On va laisser la capteur immobile pendant 2 secondes, puis on va le soulever d’une bonne dizaine de cm en le gardant horizontal (approximativement) et le poser dans les deux secondes suivantes. On va relever les mesures sur cette période de temps et les afficher. Avant cela, on va changer le format pour afficher 10 décimales après la virgule dans le script précédent.
print("{:0.10f}".format(accel.x), "\t", "{:0.10f}".format(accel.y), "\t", "{:0.10f}".format(accel.z), end="\t")
print ("{:0.10f}".format(gyro.x), "\t", "{:0.10f}".format(gyro.y), "\t", "{:0.10f}".format(gyro.z))
On obtient les mesures suivantes:
Un affichage des 3 composantes d’accélération donne le graphique suivant:
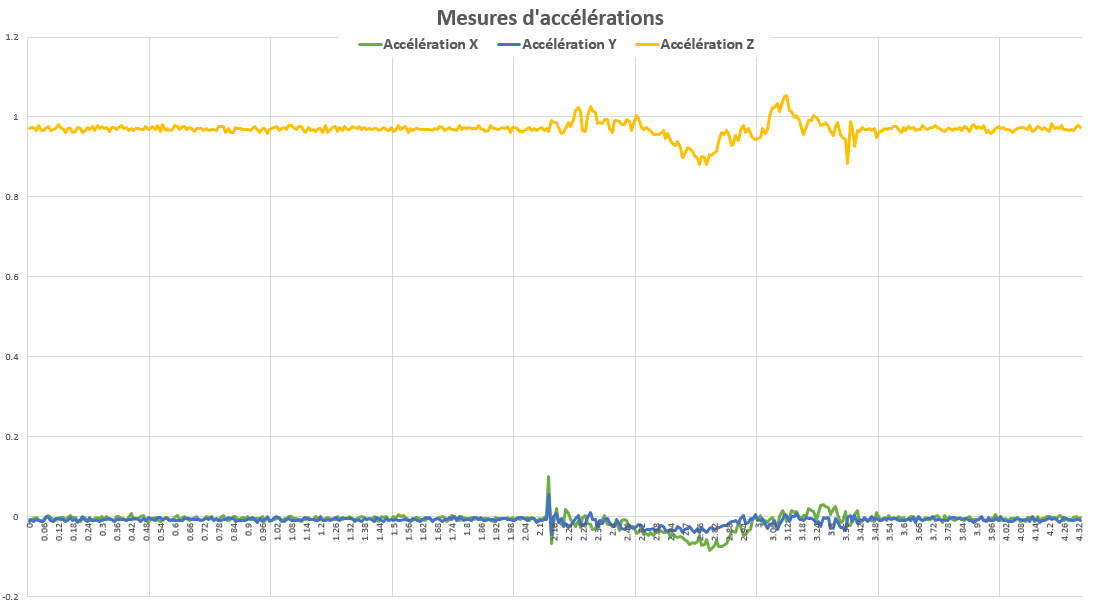
On remarque plusieurs choses:
- Les mesures de la première moitié du graphique oscillent légèrement autour de valeurs stables: alors que notre capteur était immobile, il a enregistré des accélérations. C’est notre bruit de mesure.
- Les mesures de la seconde moitié varient significativement, d’un ordre de grandeur plus grand que les petites variations. Ces grands changement de valeur sont la mesure du mouvement que l’on imprimé au capteur.
- L’axe Z évolue autour de la valeur 1, tandis que X et Y autour de 0. En fait, même immobile on mesure l’accélération de la pesanteur. Elle est égale à 1g à la surface de la terre.
Bruit de mesure et accélération de la pesanteur vont venir perturber nos mesures et nos tentatives de reconstruire une position. Observons-le: pour convertir une accélération en position, il faut intégrer deux fois les mesures d’accélération. La première intégration convertit l’accélération en vitesse, la deuxième convertit la vitesse en position. Quand on dispose de mesures, on peut intégrer de plusieurs manières, on va utiliser la méthode du trapèze, ce qui donne les formules:
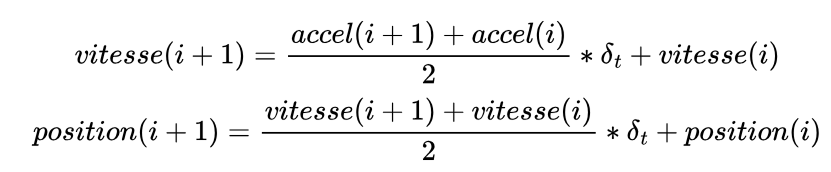
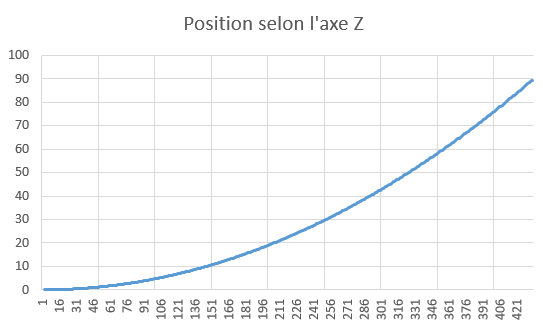
Concrètement, pour obtenir la vitesse à un moment, il faut moyenner les deux mesure d’accélérations contiguës, et multiplier par le temps d’échantillonnage entre les deux mesures (sans oublier de convertir les accélérations en g en m.s-2, en effet 1 g = 9,806 65 m.s-2 Et ainsi de suite pour la position à partir de la vitesse. Si on réalise ces 2 calculs sur les mesures, on obtient la représentation suivante.
On s’attendait à observer une valeur z qui augmente puis qui rediminue, pour correspondre à notre mouvement de montée et de descente, mais ce n’est pas le cas. En fait, la donnée brute intégrée deux fois considère la gravité qui se cumule au fur et mesure et empêche de retrouver notre mouvement, de bien plus faible importance. On arrive même à la valeur incroyable de 90 mètres: l’équivalent d’une chute libre sur cette durée (au signe près, histoire de convention). Maintenant qu’on a compris l’influence de la gravité sur notre mesure, on va essayer de l’enlever pour rendre nos mesures plus précises.
Retirer la gravité
On avance de manière didactique ici, les prochaines étapes sont vraiment le niveau 0 du traitement du signal, mais en découvrant les limites de la suite, on abordera plus sereinement les étapes suivantes. Ainsi la première grosse simplification est qu’on va ignorer les axes X et Y. C’est faux et risqué car mon composant n’étant pas strictement horizontal à tout moment, une partie de la gravité est aussi mesurée par les axes X et Y, et cette partie peut changer avec le temps comme illustré sur la figure ci-dessous.
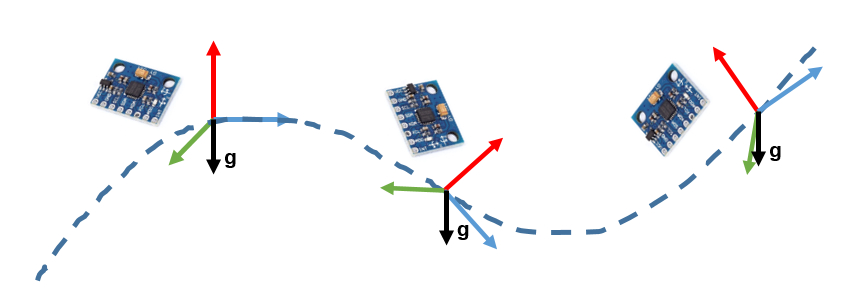
Mais traiter les trois composantes en dynamique nécessite aussi de s’intéresser à l’orientation et on ne va coupler immédiatement les mesures du gyroscope aux accélérations.
Méthode 1: on soustrait 1g aux mesures d’accélération
Nous avons compris que la gravité devait être retirée. C’est parti: la gravité vaut 1g, on retire donc 1g aux mesures d’accélération en Z, on recalcule vitesse et position et on affiche les mesures de position en fonction du temps.
Le résultat est décevant: en 4 secondes, on finit 30 mètres sous terre. On comprend qu’ici, 1g n’était pas la bonne valeur, car une partie de la gravité impacte les autres mesures. En effet, elle ne sont pas exactement nulles sur le graphique. Notre expérience faisant revenir le capteur à la même hauteur, on s’attendrait à une mesure en fin d’expérience égale à la première. Calculons la différence pour une estimation de la dérive de notre système {capteur + correction des mesures}: 6.26m soit 6260 cm par seconde.
Méthode 2: on soustrait aux positions un polynôme de degré 2
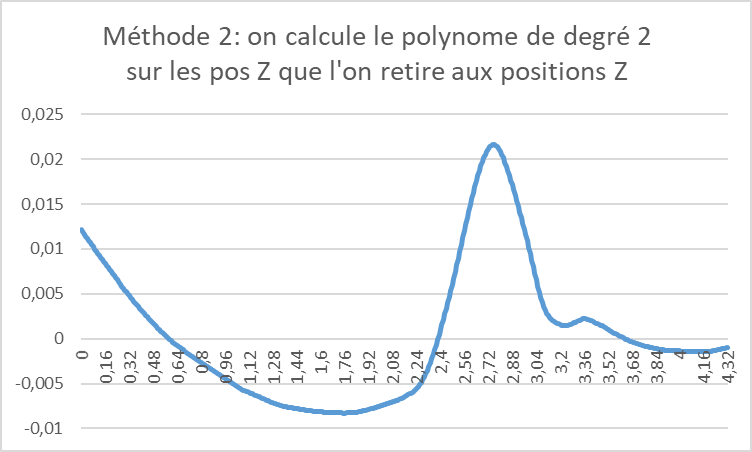
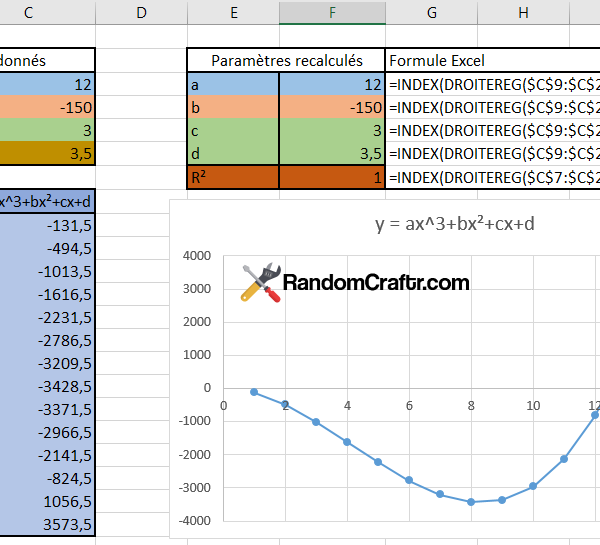
Au lieu de prendre une valeur arbitraire, on comprend bien que cette constante sur l’accélération intégrée deux fois ajoute un polynôme d’ordre deux sur le calcul de position. On essaie donc de calculer le polynôme qui s’ajuste le mieux aux données de position et on le retire. Pas forcément trivial à implémenter, mais on fournit plus loin le fichier Excel avec les mesures, les calculs et les graphiques. On observe le résultat.
Intéressant: on retrouve un mouvement qui correspond à notre expérience entre 2.4 et 4 secondes. Ca monte et ça descend, mais de seulement 2cm, pas 10cm. Et ça bouge trop au début: le polynôme ajusté sur l’ensemble des données mesurées est perturbé par le mouvement. Estimons néanmoins une dérive de notre méthode: environ 5 cm par seconde. On a déjà gagné deux ordres de grandeur avec cette méthode ! Mais pour faire mieux, il aurait fallu une phase de calibration séparée.
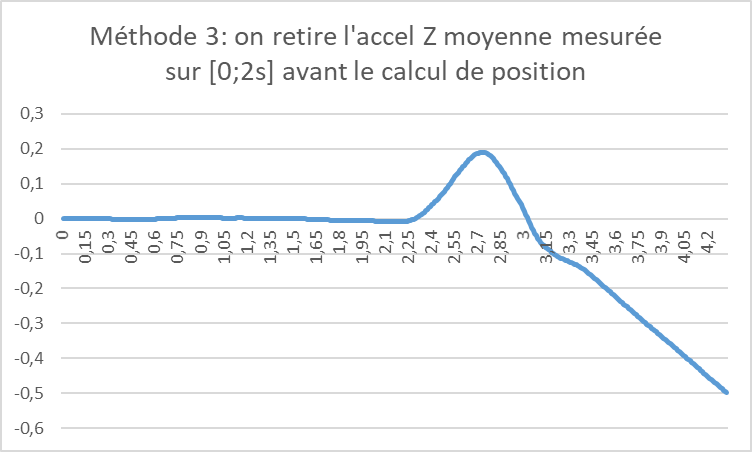
Méthode 3: on retire l’accélération moyenne sur une phase stable
A partir de ces deux méthodes, on construit une troisième: au lieu de retirer 1g, on va retirer la moyenne des accélérations, mais mesurée uniquement pendant la phase de repos. Ainsi, j’aurai la seule composante de la gravité qui s’exerce sur Z, et avec la valeur numérique exacte si le capteur mal calibré ne mesure pas exactement 1g, ou si une part de cette gravité est présente sur les autres composantes. On observe la mesure de position corrigée suivante:
Une mesure de dérive donne 11.5cm par seconde. Moins bien finalement. L’ordre de grandeur de la hauteur atteinte est plus proche de la réalité. Observe que sur la partie où le capteur est immobile entre 0 et 2 secondes, la dérive est bien meilleure: si on la calcule en prenant la différence entre les positions à 2 secondes et initiale, on obtient la dérive de 0.1 cm par seconde.
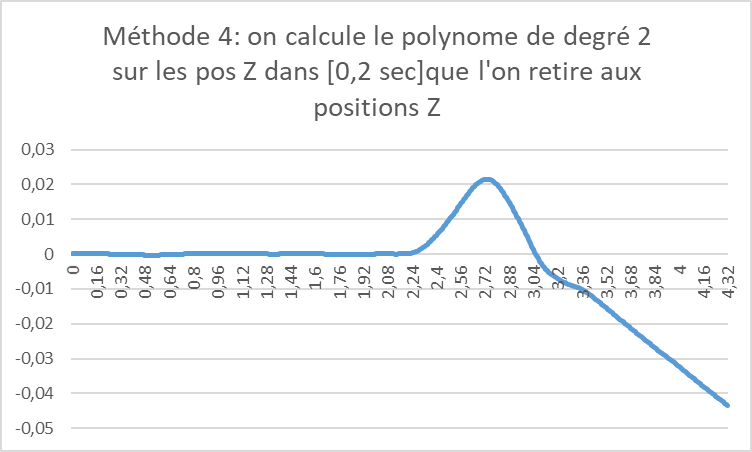
Méthode 4: on soustrait aux positions un polynôme de degré 2, ajusté sur la phase d’immobilité
Pour terminer cette première approche, on améliore la méthode 2, en ajustant le polynôme pendant la phase d’immobilité. On espère ainsi de ne pas polluer l’estimation de la correction par le mouvement qui a lieu après. Mais on retire ce polynôme sur l’ensemble des mesures, mouvement compris. On obtient la figure suivante:
La figure est très proche de la figure précédente, mais on gagne un ordre de grandeur sur l’échelle !
Synthèse des performances des 4 méthodes de correction des mesures
On résume les dérives estimées des trois méthodes, et dorénavant, on va s’intéresser à la fois à la dérive par seconde dans la phase d’immobilité [0,2 secondes], mais aussi à la dérive en mouvement dans la totalité de la phase [0,4 secondes]:
| Méthode 1 | Méthode 2 | Méthode 3 | Méthode 4 | |
| Dérive avec capteur immobile | 284.26 cm.s-1 | 0.97 cm.s-1 | 0.34 cm.s-1 | 0.01 cm.s-1 |
| Dérive avec capteur en mouvement | 626.23 cm.s-1 | 5.06 cm.s-1 | 11.51 cm.s-1 | 5.78 cm.s-1 |
Voici le fichier avec les mesures brutes et les méthodes 1 à 3. Pour la quatrième, il faut changer le calcul des coefficients du polynôme a,b,c pour qu’il ne traite que les lignes des mesures comprises entre 0 et 2 secondes.
Conclusion intermédiaire
Cette première expérience nous a permis de:
- Comprendre que la dérive mérite d’être mesurée en situation d’immobilité et en situation de mouvement
- Gagner jusqu’à 5 ordres de grandeur entre la mesure brute et la mesure post-traitée
Mais ce bon résultat n’est qu’indicatif. En effet, on a appliqué notre correction de mesure sur les mesures qui avait servies elles-mêmes à ajuster le modèle. Ce sur-apprentissage devra être résolu en créant un jeu plus large de données.
Quelques ressources
Cette page m’a donné l’occasion de consulter de nombreuses ressources. Voici les plus notables:
- Un détail du MPU6050: https://mjwhite8119.github.io/Robots/mpu6050
- Une explication du composant au cœur du MPU6050: https://lastminuteengineers.com/mpu6050-accel-gyro-arduino-tutorial/
- Une méthode pour déterminer roll/pitch juste avec la lecture de l’orientation de la gravité: https://howtomechatronics.com/tutorials/arduino/how-to-track-orientation-with-arduino-and-adxl345-accelerometer/